Operaciones entre conjuntos

Operaciones entre conjuntos

Además de relacionar los conjuntos a través de la contenencia y la igualdad, podemos crear unos nuevos a través de las operaciones entre conjuntos.  Aquí aprenderás de que se trata.

Unión de conjuntos

Supongamos que tenemos los conjuntos  y  definidos como se muestra en la siguiente figura:



Podemos crear otro conjunto conformado con los elementos que pertenezcan a  o a .  A este nuevo conjunto le llamamos unión de  y , y lo notamos de la siguiente manera: .  En la imagen de abajo puedes observar el resultado de unir los conjuntos  y .

Al elegir qué elementos estarán en la unión de nuestros conjuntos  y , debes preguntarte cuáles están en el conjunto  “o” en el conjunto .  El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal , que cumplan la condición de estar en uno o en otro.

Tenemos en este caso: :


Intersección de conjuntos

Sigamos tomando como ejemplo los conjuntos M y N definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos M y N tienen en común.  A este nuevo conjunto le llamamos intersección de M y N, y lo notamos de la siguiente manera: M.N

Nelson Hernández. PEM.

Los Conjuntos: Operaciones entre conjuntos

Operaciones entre conjuntos

Además de relacionar los conjuntos a través de la contenencia y la igualdad, podemos crear unos nuevos a través de las operaciones entre conjuntos.  Aquí aprenderás de que se trata.

Unión de conjuntos

Supongamos que tenemos los conjuntos  y  definidos como se muestra en la siguiente figura:

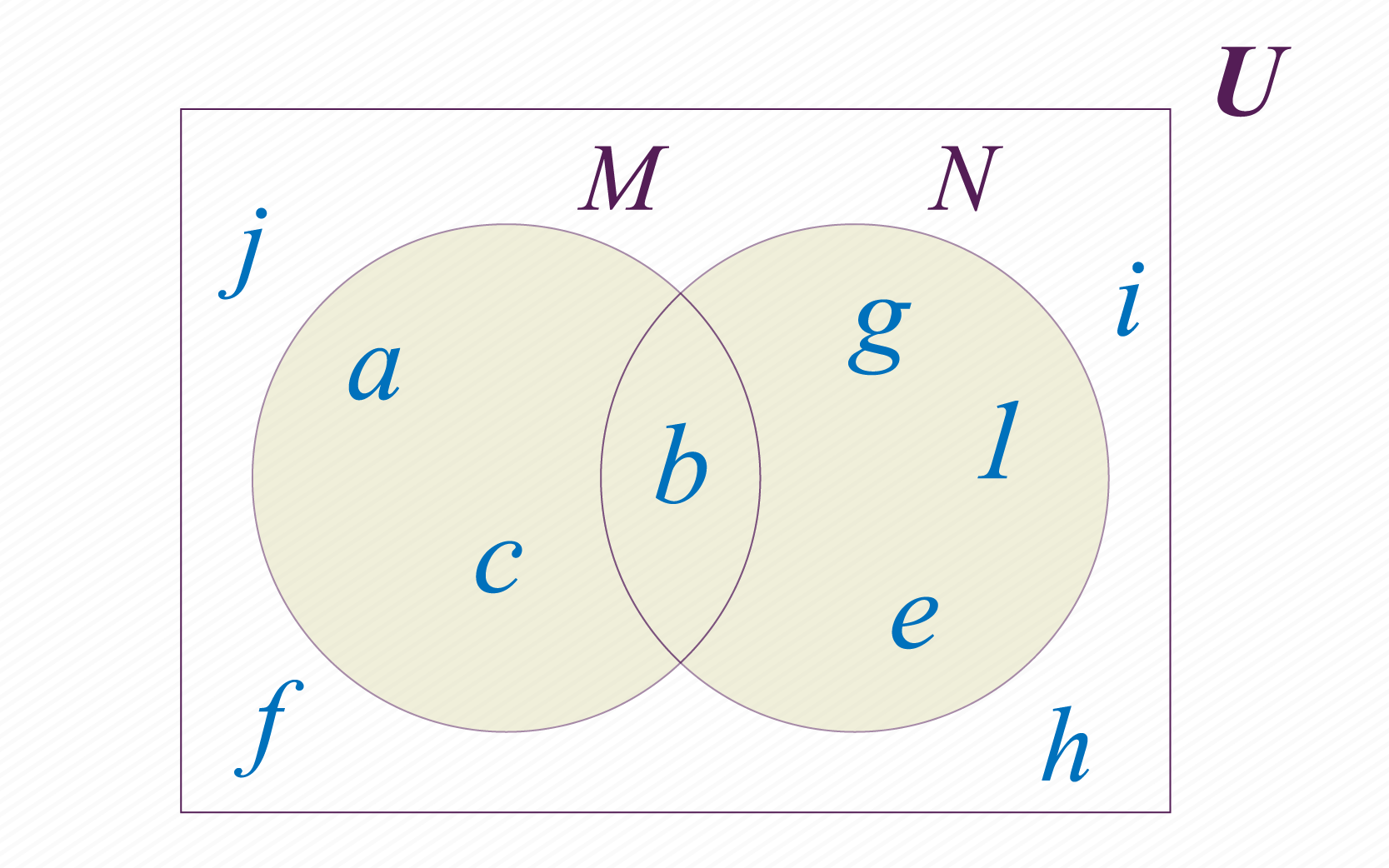
Conjuntos M y N.

Podemos crear otro conjunto conformado con los elementos que pertenezcan a  o a .  A este nuevo conjunto le llamamos unión de  y , y lo notamos de la siguiente manera: .  En la imagen de abajo puedes observar el resultado de unir los conjuntos  y .

Al elegir qué elementos estarán en la unión de nuestros conjuntos  y , debes preguntarte cuáles están en el conjunto  “o” en el conjunto .  El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal , que cumplan la condición de estar en uno o en otro.

Tenemos en este caso: :

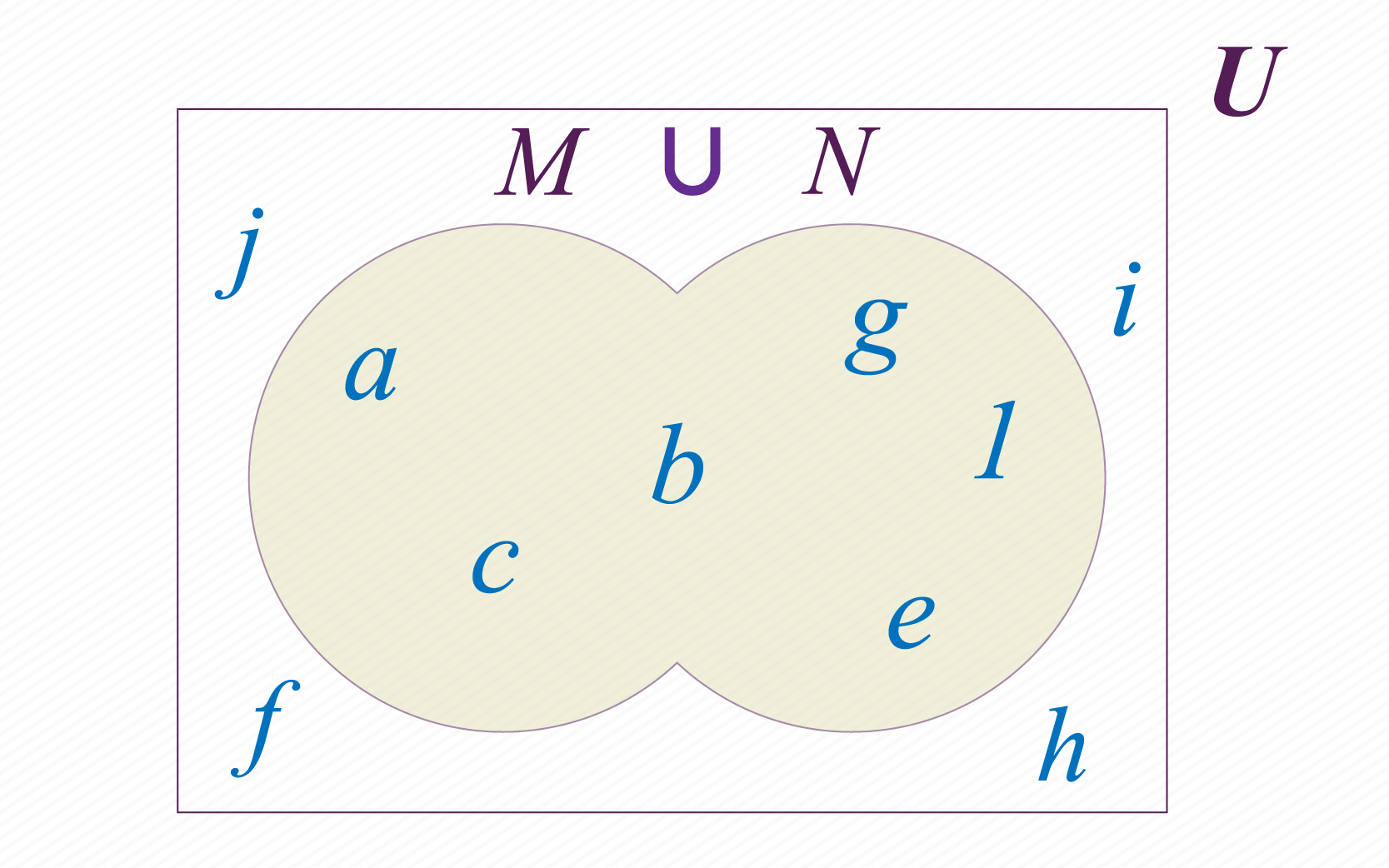
Unión de M y N.

Intersección de conjuntos

Sigamos tomando como ejemplo los conjuntos  y  definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos  y  tienen en común.  A este nuevo conjunto le llamamos intersección de  y , y lo notamos de la siguiente manera: .

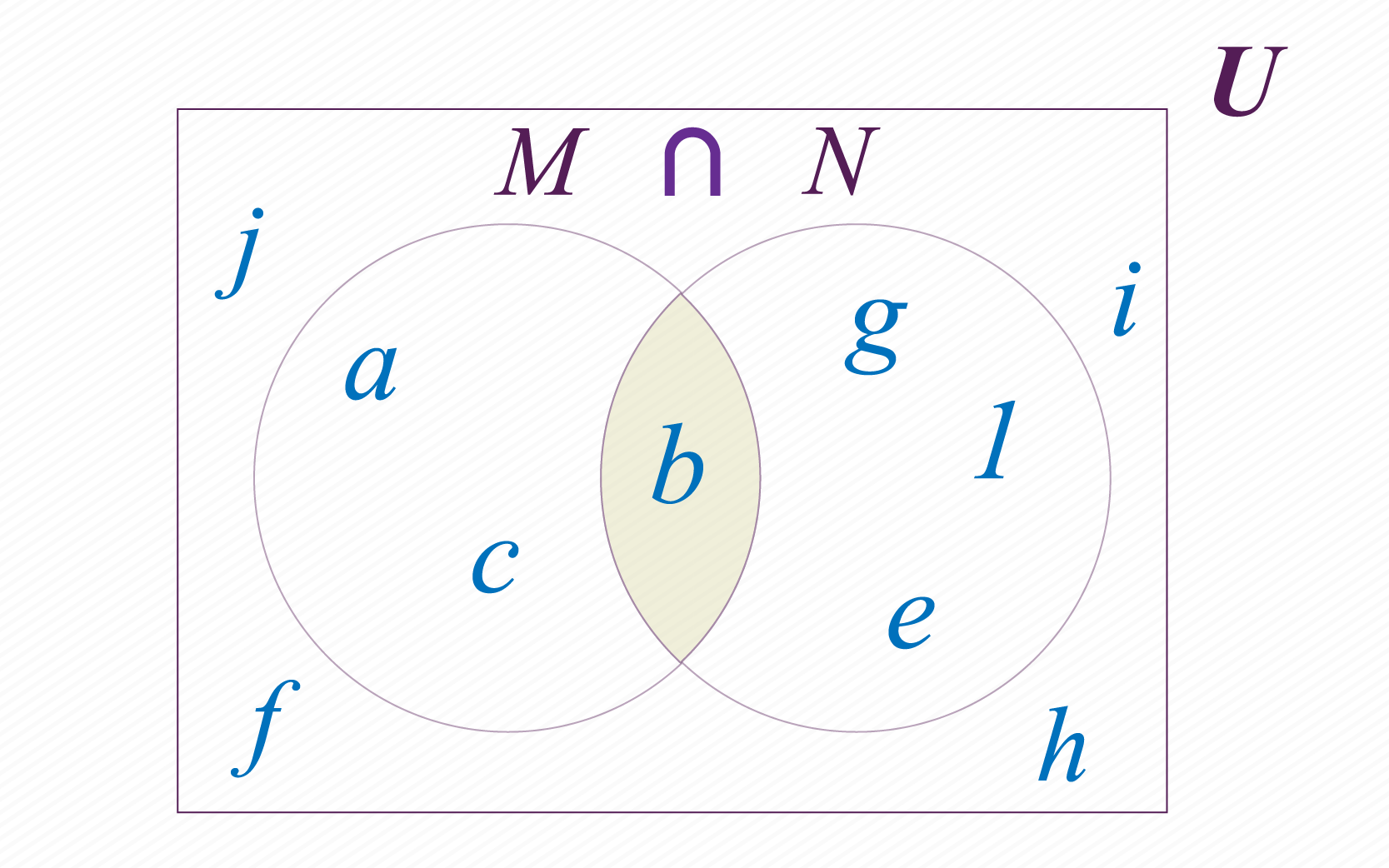
Intersección de M y N.

Para determinar que elementos pertenecen a la intersección de los conjuntos  y  te puedes preguntar qué elementos están en  “y” en   Todos los elementos del conjunto  que cumplan esta condición deberán estar en el conjunto .  En la figura de la arriba puedes ver la intersección de nuestros conjuntos  y : .

Diferencia de conjuntos

Además de la unión y la intersección podemos realizar la diferencia de conjuntos.

En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación menos , debes seleccionar los elementos de  que no están en .  Representamos la diferencia M menos N así: .  Observa que en este caso .

Diferencia simétrica de conjuntos

Que el nombre esta operación no te alarme, también es muy sencilla.

En esta ocasión se deben escoger los elementos de  que no están en , y los elementos de  que no están en .  Puedes ver el resultado de la diferencia simétrica entre  y  en la figura de abajo.  Representamos la diferencia simétrica a través del símbolo .  En el caso de nuestros conjuntos  y  tenemos: .






Comentarios

Publicar un comentario

Entradas populares de este blog

Teoría de conjuntos

Imagen
El concepto de  conjunto  es intuitivo y  se  podría definir como una "agrupación bien definida de objetos no repetidos ni ordenados"; un  conjunto  está bien definido, cuando puede afirmar si un determinado elemento pertenece o no al  conjunto. Clasificación de los conjuntos: 1) Homogéneas y heterogéneas. 2) Ordenables y no ordenables. 2) Finitos e infinitos. 3) Vacío. 4) Unitario. 5) universal o universo.           Formas de escribir un conjunto: Forma enumerativa:   Los conjuntos  en  forma enumerativa son aquellos  conjuntos  que sus elementos tienen una lista de cada cosa que esta dentro de ese  conjunto  sin repetirse. Forma descriptiva: Se representan escribiendo la característica de los elementos y se encierran entre llaves. Forma gráfica: Se escriben dentro de la figura geométrica cerrada y el nombre del conjunto se coloca fuera de la figura. Ejemplo:
Leer más

Regla de tres simple (Directa e Inversa)

Imagen
  Proporcionalidad Si la relación entre las magnitudes es directa (cuando aumenta una magnitud también lo hace la otra) hay que aplicar la regla de tres simple directa. Por el contrario, si la relación entre las magnitudes es inversa (cuando aumenta una magnitud disminuye la otra) se aplica la regla de tres simple inversa. ¿Qué es la regla de 3 simple? La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa. Para hacer una regla de tres simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad. Regla de 3 simple directa Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa (cuando aumenta una magnitud también lo hace la otra). Colocaremos en una tabla los 3 datos (a los que llamamos “a”, “b” y “c”) y la incógnita, es decir, el dato que queremos averiguar (que llamarem
Leer más

SISTEMAS NUMÉRICOS

Conjunto de símbolos y reglas que se utilizan para la representación de cantidades. Un sistema de numeración se caracteriza por su base, que es el número de símbolos distintos que utiliza para la representación de cantidades. Sistema numérico y sus símbolos: Sistema binario; 0,1  Sistema octal; 0,1,2,3,4,5,6,7,8 Sistema decimal; 0,1,2,3,4,5,6,7,8,9 Sistema hexadecimal; 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F Factores de un sistema numérico                  Operaciones Binarias Básicas: Suma, resta, división y multiplicación. Aplicación en las operaciones binarias: • Propiedad conmutativa. •Propiedad asociativa. •Propiedad distributiva.
Leer más